We began this journey using paper circles to explore the nature of matter and energy. Taping them together, we examined the idea that energy is a two dimensional phenomenon. Because we do not live in a 2-D world, this concept may not make sense to us at first. So we demonstrated it with paper circles. We made models of the saddlemniscus, or saddlem for short and use the abbreviation "S∞". (The infinity symbol is of the form known as a lemniscate.) We used the models to demonstrate how matter and energy are related. The S∞ begins as an infinite, two dimensional sheet, the veil. The veil is twisted until its center transits into a three dimensional point, the nexus. It has mass but no thickness. It is shown to have a density gradient and to be space filling. We model this concept with paper circles and cellophane tape. I encourage you to build some yourself. Instructions are found in "Basic Unit of the Universe" . Other articles in this section of the website also relate.
Now let us see if the S∞ can describe the atom. First of course, we will consider an atom of one proton and one electron, the hydrogen atom. Then we will show how neutrons and the larger atoms are described. It is an easy matter to say that the three dimensional nexus at center represents the proton. But how does the electron come to be, and why is it so different from the proton? To do this we will have to separate the veil so that our proton and electron can operate independently. Then we will have to demonstrate how mass can be accumulated to form the electron. We must also account for the changing position of the electron.
In the article "Density", we describe how the S∞ has a density gradient towards its center. In the article on "Force", the density difference ratio, DDR, is explored in detail. There is a gap in the DDR graph at the unit value, x= 1, whose y value is "nan" is not a number. True, the value of x at 1 is only a point. There is also a corresponding value of y, which is less. Taking the derivative of the DDR on either side of the gap, it implies that y would be ¾ of the value of x. The x scale represents distance from the center, so the form of the nan gap is a spherical shell in the space filling veil, centered about the nexus. I am not saying that the veil does not exist in this gap. It is still there. I am suggesting that the Density Difference Ratio does not apply at unity.
A rationalization for the nan gap in the DDR is this. We allow the veil to have mass. If the S∞ is infinite in radius or even just quite huge, there will be a balance point between the concentrated mass of the very soupy core and the more tenuous mass of the outer reaches. At that radius, there will be as much pull on the veil to go inwards as to go outwards. The amount of veil beyond the spherical gap is vast. There must be a sphere of some radius between the center and the outer limit that is in equilibrium. I contend that this sphere is located at the nan gap. We will also refer to the unit value as the "first harmonic". This concept has a counterpart in a region of space surrounding our solar system. There is some distance from the sun where the inwards gravitational pull of the sun and inner planets is just matched by the pull of the rest of the universe outwards. A body at this radius equally feels tugs towards the sun and away from it. The spacecraft Voyager may be near that area now. I am suggesting that the electron resides in a similar locale. Even within our solar system there are a series of locations called Lagrange points between two large bodies like the Earth and the Sun where a third body, like a spacecraft, can find equilibrium. That is where solar observational satellites stay.
Effectively, we are dealing with two entities. The central nexus and inner skirt of the veil are one. The electron shell and outer veil are the other.
In the "Density" article we developed the concept that the density of the inner portion of the veil is always higher than the density of the outer portion. There is one exception, here. As we have surmised above, there is a void in the DDR of the veil at unity. Its circumference on the far side of the gap must be larger than the circumference at the inner side of the gap. That allows it to "wrinkle".
Allow me to present a simplification that, while not quite accurate, may help introduce the concept we seek. First fold a sheet of paper into a simple "S". Just take a sheet of paper and fold it in half, then take the top half and fold it back over the crease. If you hold it up and look at it along the edge it takes the form of an "S" or "Z". Take another sheet of paper and draw a circle on it. Can we make an S fold around this circle? This would be very difficult to accomplish with paper. But it can be done with cloth. The photographs show a bed sheet tucked over a glass plate. A couple of magnets have been placed on either side of the center of the plate to represent the nexus.

Notice how the cloth bunches up around the rim. This is simply because there is more sheet in the outer circumference of the rim than at any lesser diameter. In the S∞ model, the sheet represents the veil. The plate and magnets at the center represent the skirt and inner nexus. I do not believe that the sheet of the veil really forms an S bend. It is not necessary because our first harmonic gives us a place for the veil to cumulate mass. For the electron to become an independent entity, it is necessary for the veil to separate. The nan gap allows its outer shell to collapse upon its inner shell.
When we first started making the S∞, we saddled up the veil. This allowed us to compact the 2-D veil into a 3-D nexus. Similarly, this process allows us to concentrate mass at a radial distance from the nexus. That mass is the electron.
Most descriptions of an electron do not represent it as only a simple point, like a planet orbiting the sun. Rather it seems to be like a cloud sometimes. The cloud describes its probability of being in a particular location. These most likely locations are called orbitals. A couple of excellent websites describing orbitals are http://www.orbitals.com/orb/orbtable.htm and http://www.shef.ac.uk/chemistry/orbitron/. The location of the electron is quite variable. So, if our model is to represent it, it must be capable of a similar fluidity. Where can we locate it on the veil of the S∞?
To illustrate this, the following photographs were taken of a ribbon from a paper saddlem placed around a glass globe. In the first photo, the ribbon was distributed all around the globe. In the second it is beginning to bunch around the top. In the third it has been tightly rolled. It is the same ribbon in all three, never cut, just configured differently. An external force (me) pulled them to different configurations. We describe how to make this ribbon in "Unit of the Universe Basics" and refer to it in "Photon in a Fishbowl" and "DNA Demonstrator". If you have made a saddlemniscus, you can follow the instructions to make a DNA demonstrator. Then use the ribbon to do these yourself. The ribbon represents the concentration of mass in the nan gap. So you see, it is not really wrinkled like the sheet.



Consider the electron to be a standing wave at a more or less stable distance from the central nexus, the proton. The mass of the electron develops from the wave´s nature - its effect upon the veil. The electron has mass because the veil has mass and the wave concentrates it at the first harmonic. Let us look at how the model of the S∞ allows for that.
The electron has a mass much smaller than that of the proton. It surrounds the nucleus. It has a variety of configurations. It has different energies and seeks the lowest energy. Importantly, it can be separated from its proton and they can operate independently of each other.
Recall that in "Intermediate Unit of the Universe" we showed different states that the S∞ can take. One is the spiral form, another is the ruff. The spiral form in Figure 6 shows the proton center and electron shell. The proton-nexus is completely surrounded by the electron shell and veil.
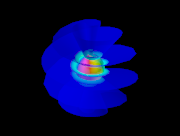
As energy is taken in, the form goes through the whorl phase. Here the helical planes of the veil become wavy. Eventually the wavy portion dominates and the S∞ is completely in the ruff phase. In the ruff phase, it has an opening at the poles. In that configuration, the proton has a way to escape. If you have ever used a tool to remove a cherry or olive pit, this may look familiar.
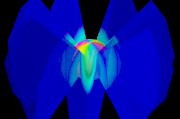

Figure 8. Separation of the Proton and Electron
The nexus has become an independent particle along with the inner skirt of veil remaining with it. The electron shell and outer veil then behave as a unit. With no proton, the inner edge of the electron shell can further compress into a tinier sphere, concentrating its mass about a center. At the center is the only true nothing in the universe. Remember that in our system, the universe is filled with innumerable veils of other saddlem. It is what other systems call dark matter. We do not allow any empty space but these central voids.
How far outwards does the electron extend? After all, the veil is infinite in extent. Moreso, we have described the photon as using this property to shine across the universe. This gives a huge problem. Namely how could it possibly assume the variety of shapes we have demonstrated with the ribbon in Figures 3, 4 and 5 above and remain space filling. To answer this, first recollect that when the nexus was formed in three dimensional space it acquired mass and became a different sort of object than the veil from which it was created. We have done a similar thing with the electron to give it mass. As we have described it, the electron has a nature somewhere between veil and nexus. It extends outwards to the second harmonic. The first harmonic is the nan gap. Between it and the farthest extent of the veil there will be another sphere of equilibrium, the second harmonic. That is our extent. More on this when we deal with larger atoms.
Do the veils of other S∞ penetrate this ball of nothing? No, they must distort around it. Here we have added new properties to the veil that have not been dealt with in previous articles.
The electron shell now can exist as an independent entity. It can jump to different energy states without reference to a proton or the remainder of the veil. As a free electron, it is capable of existing at low or high energy states. It can relax back into the spiral phase or wind itself into a point.

As long as there is still a short skirt of veil about the nexus, it is not purely a proton. It would have a slightly higher mass than a proton. I believe that this is where the neutron originates. The remaining veil is a shell that begins virtually at the boundary of the nexus. It extends out to the nan gap. It stays in place unless affected by a sufficient force. It then departs as a neutrino or other form of mass/energy equivalence. That leaves the proton of the nexus.
This implies that the neutron is more primitive than the proton. There is of course a time when these came into being and a process by which that occurs. That will be dealt with in a future article. What we showed in Figure 8 is a primordial or first time separation. Ordinary atomic processes are mature combinations. Remember, these particles have been separating and recombining for billions of years.
Meanwhile, this free proton is muscling its way around the sea of other veil-nexus combinations which comprise our universe. A proton has mass, but so does a veil. So do all veils. We defined the nexus so that no more veil could be added. It cannot become more three dimensional than it is. We do allow the surrounding region to become soupier.
So we must answer the question, can the three dimensional proton-nexus occupy the same space with a two dimensional veil - even over the tiny space that the proton occupies? No, it will always have some two dimensional shadow in the same plane as any two dimensional veil. In observations of light going around massive objects, it appears to bend. So the veil will not share the same space as a proton-nexus. The nexus transitions to 3-D space just because it cannot compact any more veil into itself. That means that it cannot collocate with veil. To move around through space the proton pushes veil aside. This will create a certain local distortion in space as density increases. It will have a net outwards effect from the proton.
Returning for a moment to the electron, since it has now also transitioned into a 3-D object, it would also forbid the penetration by additional veil. In its free form, it has collapsed around the void hole. So its net effect upon the surrounding veil will be to pull it inwards. The distortion will be the opposite of that created by a proton. It is this opposition in effects that creates the draw between the two.
Next, consider what happens when a free proton and a free electron combine. We said above, the interior of the electron contains the only true nothing in the universe. There are two places that veil cannot be. One is the center of the electron and the other is location of the proton. One is three dimensional nothing and the other is three dimensional something. This is the origin of attraction and repulsion. Plus and minus in our system are something and nothing seeking resolution. Two electrons have nothing to offer each other and so repel. The same is true of two protons.
There is no intrinsic attraction between proton and electron once they are joined. The electron has no further urge to merge with the proton. It is happy to be where it is. Only when the two attempt to separate does charge come into play.
We no longer have the skirt of the neutrino. It went away somewhere when the neutron broke apart. Even after the proton and electron have joined, they are still not in perfect balance. The proton has lost veil when its primordial configuration split. The electron did not. Its mass resides at a closer radius now than in the primordial. It will still have a net pull on the surrounding space. The hydrogen atom is electrically neutral so this is not reflected as excess charge. This pull I believe is the origin of gravity. The distortion seems to be cumulative, as greater numbers of atoms produce a proportional effect.
Why does the electron still have a radial distance from the proton? What keeps it from collapsing onto the face of the proton? It would seem that they would join their masses together to form a single neutral particle. That would bring us round in a circle to where this argument started, a primal particle. The electron has a net draw on the surrounding soup of veils. Once the proton has lodged at its center it can provide some satisfaction to that draw. It has a much larger 3-D mass than the 3-D mass of the electron. The proton no longer is pushing its way through the sea of veils. It is sitting in an orb of nothing. It unwinds to produce the necessary soupiness to fill the void and that keeps them separate. After all it is made of veil in the first place.
We saw some of this with "Force". That was in the effects on the rail of the closeness or distance of the two bodies. I have been considering that the Rc type relationship we described between two separate particles may apply within a proton-electron pair. In this case, the rail is spherical. In discussing Rc in force we said, "... in i2 is the potential available and in Rc is the capacity to handle it." Rc now becomes spherical between these two.
A lot has been written on the way electrons and protons come together to form larger atoms. The earlier references on orbitals gave some sources and any good search engine will give lots more. A readable explanation in greater depth can be found at http://www.chemguide.co.uk/atoms/properties/atomorbs.html. I won´t try to top their stuff or the excellent work of the many other authors.
Electron shells exist at different radii. The closest shell inwards is called the 1 (one) shell. In hydrogen there is one electron in this shell. It is said to be in an s type (spherical) orbital. In helium, a second electron joins it along with a second proton in the center. It also has an s shaped orbital.
With the proton separated, the free electron consists of the concentrated ribbon like shell at unit distance in the DDR surrounded by the veil beyond. The veil has a small mass. So the sum total of that mass beyond the shell will find a second shell at the spherical center of mass of the system of the electron. That is the second harmonic. This is where I place the number 2 shell, the next electron shell outward. This same process continues for the other shells. Eventually a harmonic is reached where the veil simply cannot congeal into a workable shell of mass.
The helium atom is the second member of the periodic table and consists of two electrons in the first shell and two protons. In the article in this series, Intermediate UU, we showed how two veils can exist with the same center. They are their own doubles. Now that we are bringing these ideas to the atom, this allows us a way to explain Helium. The second electron forms from the second veil, the double of opposite chirality. We allow it the property of an opposite spin to the first. We have discussed how an S∞ can be wound dextro or levo. The double of a S∞ is illustrated in "Dimension Part 4".
So we have a way for two electrons to exist in the same shell. What about the two protons? Because each is distorting the space around itself they have a tendency to repel each other. Like charges repel. What property of our system allows them to stay close enough to bind together into an atom. I believe it is the same configuration that allows an electron and proton to bind together in the first place as we have illustrated above. Only now, with two concentric electrons there will be two concentric voids at the center. They contain the two protons against their mutual repulsive tendencies.
The second shell, 2, has room for 8 elements. Its first member is Lithium and its last is Neon. The electrons first occupy the two available s orbitals in the 2 shell. Additional electrons assume the p orbital configuration, also in the 2 shell. Our system of the S∞ accommodates this nicely. In "Dimension Part 4" on this website, we illustrated the three sister S∞. Each of them also has its own double. That is how they would account for the six p orbitals in three pairs of two. Additional shells of even heavier elements would proceed similarly.
Atoms bond to each other in various combinations to create molecules. It is a larger topic than I wish to explore here and much material exists on the web. The Chemguide source listed above has some nice explanations. But before we close this article, I would like to show how, in the system of the saddlemniscus, one electron can be shared by two different atoms. Most of the schemes for bonding rely on electrons acting as links between atoms or molecules. This is a simple matter for the electron as we have described it. The illustrations below are of the same paper ribbon we photographed for Figures 3, 4 and 5. It was merely unwound at one end, stretched out and rewound. Then each end was attached to a fishbowl. Our little paper toys have the ability to explain matter, energy, atomic structure and molecular bonding. There is more to it of course but that will have to wait for another time.


*************************************************************************************
All images and text copyright 2005 J.M. Mongan, Oak Park, MI