First compare the areas of the outer (A) vs the inner (a) halves of a unit circle of radius, r = 1 inch.
Since π * r2 is the area of the full circle, it is simply = π
π * (r/2)2 is the area of the inner half circle; a = π/4
So the area of the outer half (ring) A, is π - a = 3/4π or three times the area of the inner.
Assign an arbitrary mass of 1 ounce (oz.) to the circle.
M = 3/4 oz. (outer half)
m = 1/4 oz. (inner half)
Now let us assume that our unit circle is surrounded by a unit sphere (r = 1) whose volume is
4/3π * r3 = 4.1888.
Compare the volumes of the outer (S) vs the inner (s) halves of the sphere.
Note: The outer half is a shell whose thickness is a half of a radius
The volume of the inner half s = 4/3π * r3/8 = π/6
The volume of the outer half shell S = 7/6 * π = 7π/6
So the outer half is seven times bigger.
The density is the mass per unit volume so:
The density of the outer shell of the sphere D = M/S = 9/14π oz per cubic inch.
The density of the inner half sphere d = m/s = 3/2π oz per cubic inch.
So the inner half of the sphere is over twice as dense as the outer half.
This process can be continued indefinitely. We could work inwards by taking the inner halves of the circle and the sphere and making 1/2 r the new unit. Conversely, we could make r = 1 the radius of our inner circle and sphere and work outwards. It is easy to see that we have a density gradient which increases toward the center and decreases as we go outbound. What are the upper and lower limits of this process?
Would the outbound limit be zero density at an infinite radius?
Would the inbound limit be infinite density at the center point?
Consider now our saddling process. We are taping together circles of paper. As we add circles to our bound helix (see UU Basics) we approach an upper limit of infinite degrees. Saddling this up would create an infinite saddlem or sphere as eventually we would cover every point on its surface. Since each of our circles demonstrate a density gradient, so then would the whole.
By extension we can say that an infinite saddlem has the characteristics of a sphere with infinite density at a point center and zero density at infinite radius.
DENSITY - Part 2
July 14th, 2003
Relative Density - The Density Difference Ratio
>INTERMEDIATE UNIT of the UNIVERSE While writing Intermediate Unit of the Universe, I began to question many of the things that I was saying. My own sanity was among them because I do say some drastic things. Primarily that matter is derived from a two dimensional sheet with mass but not volume. The density argument is pivotal. What bothered me most is the above math. It implies that if I put a sheet of paper inside of a plastic sphere, then it would somehow be magically more dense at the center. This is obviously false because, after all, it is the same sheet of paper as it was before. Is the argument flawed, I asked myself.
So, I decided to see if I could prove myself wrong by generalizing the math. Here it is. Instead of using only 1/2 of the radius, we will investigate the more general case of 1/n th of the radius, where n can be any number. We will assume that the circle is a disk cut from the veil of a saddlemniscus and has area and mass but not volume. Again we will place it into a sphere which contains nothing else. This is similar to measuring the density of a region of outer space. In space we could look at a region and count the number of atoms in it. Then we could come up with a mass for those atoms and compute the average density. Here, we will be using a disk of our veil in a sphere.
This is very similar to what we did above. Take the atoms of the inner circle of paper and distribute them evenly throughout the inner half of the sphere. Then take the atoms of the outer ring of paper and distribute them evenly throughout the outer shell of the sphere. Using our figures from above we will be 2 1/3 times more dense in the inner half than the outer. This is the Density Difference Ratio, DDR for our half radius. Next I realized that there were two different kinds of density. This kind is only relative to the position of the sphere. Let us look at it in the more general sense.
Here n is the denominator of some fraction of the unit radius, i.e. 1/n. Above n = 2. It is taken from the center outward. So, the dividing point on the unit radius moves closer to the center as n increases.
First, we will compare the ratio of the areas of the outer ring to the inner circle.
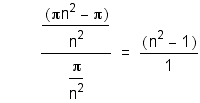
Next, we will compare the ratio of the volumes of the outer shell to the inner sphere.
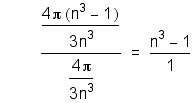
Take the area to be the mass and calculate the density of the inner sphere (assume a unit mass).
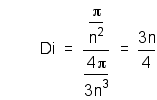
Now, calculate the density of the outer shell (assume a unit mass).
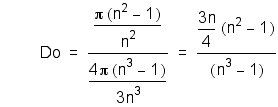
Last, we examine the ratio of the density of the outer to the density of the inner, the Density Difference Ratio.
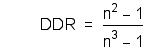
12/2/04 Hipnote: If you have read the article on Force, you may have noticed that the DDR equation is different. The variable is x and it is equal to 1/n. N as we mentioned above is the denominator of a fraction. X is the fraction directly. Also the ratio has been inverted to show the inner over the outer. Hope this didn't cause confusion.
The saddlemniscus is described elsewhere as being an infinite two dimensional veil with a point center, the nexus. As is shown above, the DDR is inversely proportional to n. Picture a tiny point in the center of a vast sheet reaching farther than the stars. Now imagine the inner circle surrounding this nexus and the enormous difference in the ratio. This is not what common sense would tell us. After all, we haven't done a thing to our density. It is still uniform throughout. All we have shown is a relative difference that only depends upon n. To get to the true picture we must examine the other type of density.
Absolute Density - The Point Centered Helix
We determined that if we added more circles, it would increase the density but not change the density difference ratio. Consider what is happening at the center. We have a bound helix. It is like all the circles have the same center point. We show in Intermediate UU the various forms a saddlemniscus can take. We also explore how it can be space filling if an infinite number of circles/degrees are taken. Our illustrations show figures with a radius of one. If you imagine them all filled up they will look like a ball, with a continuous surface. Now imagine that we take two radii from that infinite saddlem that are right next to each other. Extend their lengths by 100 times. I think you will see that they do not stay adjacent. You can see this with radii of any circle. They diverge by their nature. Space develops between them. So if I considered the radii from the ball of r =1, extending them all to r = 100 would give me a bunch of unconnected lines. I would have lost my surface.
Compare the densities of the first ball and the second ball. It would be obvious that they were not the same. (Yes, I would have to allow mass to the radii to do that, more on that later.) To heal the surface and fill it up we would need to add more radii by adding more veil. In doing so we would also be adding more veil to the inner ball. We would increase its density. The outer could never catch the inner. Every time we extended our radius we would be increasing the density of the inner. By the time we achieved an infinite radius, that would give us an enormously dense innermost ball.
The relative density of the DDR allows our center, the nexus, to travel anywhere. Absolute density allows density to concentrate at that nexus regardless of where it is. I maintain that it is enough to drive the nexus into the third dimension where we perceive it as matter.