Poppycock, the Unit of Universe offers an alternative, a rational system of physical processes that is easily demonstrable with simple materials. It is related to classical geometry and trigonometry in a straightforward manner. However, it does take the approach that what we perceive as the solid physical universe is an expression of a more planar reality. I have gone so far as to say, "Energy is a two dimensional phenomenon as viewed from a three dimensional platform". So what does that mean?
Consider that the ancient view of physical reality is based upon the most direct of observations. Matter is hard stuff. Now we think of it as little packets of subatomic somethings which can express as either matter or energy. At the subatomic scale there is a lot of room between them. So what we experience as hard stuff is not so at the smallest scale we have been able to investigate. It is composed of little packets of something we can detect swimming around in something we cannot detect and therefore call nothing. The words "field" and "energy packet" come up a lot but there is not an image our minds can readily latch onto. There is no geometric basis with which we can identify.
So here is my point; we look at physics as the study of three dimensional objects which have been given a kick in some manner to set them in motion. So we proclaim this to be our model of reality and go from there. I am saying that it is just as valid for two dimensional forms projected through time to result in what we perceive as reality, or more properly, to serve as the model for physical reality. We do this with the simple models described in other areas of this work. The object now is to show a correspondence in a classical light with the hope of legitimizing these wild assertions. Let us begin with the equilateral triangle.
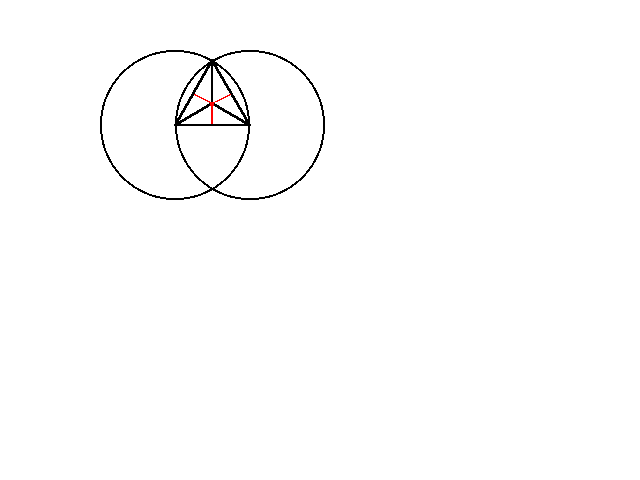
Figure 1 The equilateral triangle
Consider this to be the top view of a regular tetrahedron. Seen as a solid figure it looks like this.

Figure 2. The tetrahedron
If we add a second equilateral triangle to the first, its double, but pointing in the opposite direction, it will define a hexagon. The hexagon in turn can be considered to be a view (not the top view) of the cube or regular hexahedron. Figure 3 demonstrates the projection of a hexagon to a cube. I guess you could also take it the other way around - the back projection of the cube to a hexagon.
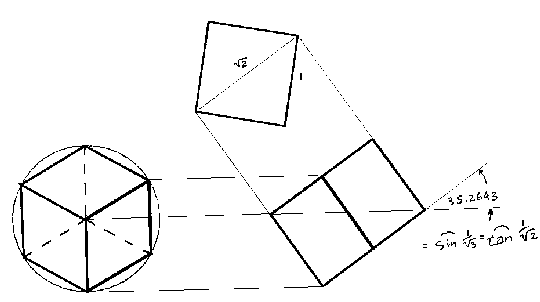
Figure 3. How the hexagon projects a cube
Since a hexagon can be defined by an opposing pair of triangles and those triangles are each 2-d glyphs of tetrahedra, is that reflected in the cube also? Yes it is. First let us take a closer look at the tetrahedron. It is fractal. Figure 4 shows lines connecting the midpoints of the edges. Cutting along planes defined by these lines will separate it into four half pint tetrahedra.
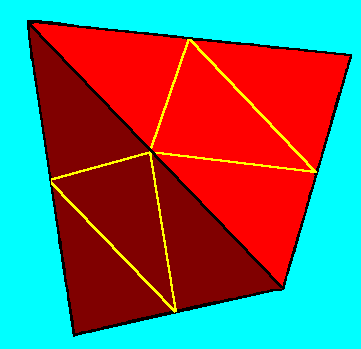
Figure 4. Connecting the midpoints
There will be a central part remaining. It is a regular octahedron.
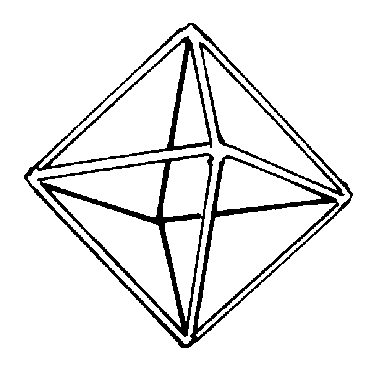
Figure 5. The octahedron
We defined it with four half pint tetrahedra. The octahedron has eight faces, each an equilateral triangle. This leaves four free faces which could be used to define the doppleganger of our original tretrahedron, the full pint. The double of a solid is achieved by putting a vertex where a face is on the original. Interestingly, the double of an octahedron is a hexahedron or more commonly, a cube. A cube, of course has six faces and eight vertices, just the opposite of the octahedron.
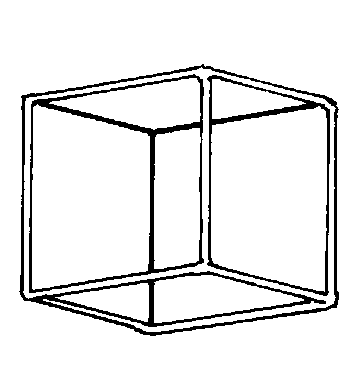
Figure 6. The cube
Since a cube is a regular figure, all of the diagonals of all of the faces are the same length. This allows a tetrahedron to share four of its vertices in the following manner. The edges of the tetrahedron occupy six of the possible twelve diagonals.
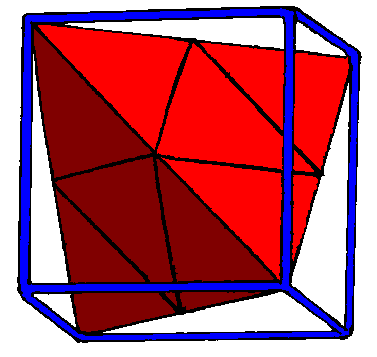
Figure 7. The nesting of a tetrahedron in a cube
Notice how the tetrahedron also only occupies four of the eight corners of the cube. It should also be fairly apparent that the unoccupied corners are opposite to the exposed faces of the octahedron.

Figure 8. The open faces of the octahedron
These are the faces we defined above by connecting the tetrahedron's midpoints. Since those are also equilateral triangles, we should be able to put half pint tetrahedra on each of them. This defines the original tetrahedron's double. We can now say; "An octahedron is the volume common to a tetrahedron and its double. A cube is the volume defined by their extremities." I have come to call this figure the "Silver Solid".

Figure 9. The dual tetrahedra define the cube The SILVER SOLID
Note that it is fractal. Each of these half pint tetrahedra can be the starting point of their own silver solid. Each of the full pint tetrahedra can be the half pint to a tetrahedron that is even larger yet.

Figure 10 The fractal nature of the system
In case you haven't guessed, there is yet another point of view to this process. That is to understand the tetrahedron to be the resultant of projecting the equlateral triangle through time. To assist with the visualization of this heresy, let's use a version of the prism. In this case it would be like a triangular prism. To avoid confusion with a true solid prism, I prefer to call it a tridrum, like a drum with three rectangular sides and two equilateral triangular ends. A hexadrum would have six rectangular sides and hexagonal ends, and so forth. The tridrum is to be considered a frame of reference for projecting the triangle through time. One end of the tridrum has the etching of the triangular base of a tetrahedron. The other has but the dot of the apex. It is as though time's arrow has struck at the center of the base and drug it outwards, pulling the triangles bisectors with it. This is what I mean by the projection of a two dimensional figure through time. Each point along each bisector would have a temporal vector corresponding to its counterpart on the tetrahedron.
Look again at the cube et al. as the projection from the hexagon with its diagonals and chords. The hexadrum would only demonstrate an apex upon each of its ends. Between them all else resides.
The start of this article demonstrated using one dimensional lines to define a two dimensional figure which is then used to define a three dimensional solid. The central point however, is that in previous work I have redefined the tetrahedron as a curve in space, a harmonic along the sequence that runs point, line, cone, circle, saddlemniscus (see UU Basics), sphere. I call that the "Unit of Universe". It is that one special saddle whose maxima and minima define the regular tetrahedron. It is shown as the introductory picture at this website's home page. It is simpler in that one tetrahedron can be defined by any of three saddles, equal in all else but orientation. With its double, the cube is defined and so forth. This saddlemniscus can be considered the distortion of a plane through time.