In the articles Force, The Atom and Electricity, Electromagnetism and The Licosas the rail was introduced. The rail is proposed as a means for the transmission of energy from one saddlemniscus to another. Each saddlemniscus, abbreviated S∞ , is considered to be space filling and so has radii in every direction. So even when two S∞ are in motion relative to each other, they will always share one collinear radii even though it is constantly changing. Rails occur at these collinear radii. Rails come from the conch. The conch is a new geometric form to this series and is described below.
First, the usual caveats. This is not mainstream science. It is an exploration of a geometry which assumes twisted two dimensional sheets can be used model reality. It asks what if this geometry was tasked to describe various physical phenomena. Would it have an explanation for time, space matter and energy? I am not saying that space is composed of twisted two dimensional sheets. S∞ are described elsewhere in this series, Unit of the Universe. There is something out there. Light travels through it. Light has properties of a wave. Waves travel through a media. But I digress.
In the world of the S∞ we have described the SPIRAL form. Its radii are all linear. Here we introduce the CONCH. Its sections are all curved. As we use it here, a conch is generated by the rotation of a planar spiral about an axis. We will define a specific CONCH by a parametric equation in spherical coordinates r, theta, & phi. The variable is n. The parameters are u and v.


Figure 1. Conch

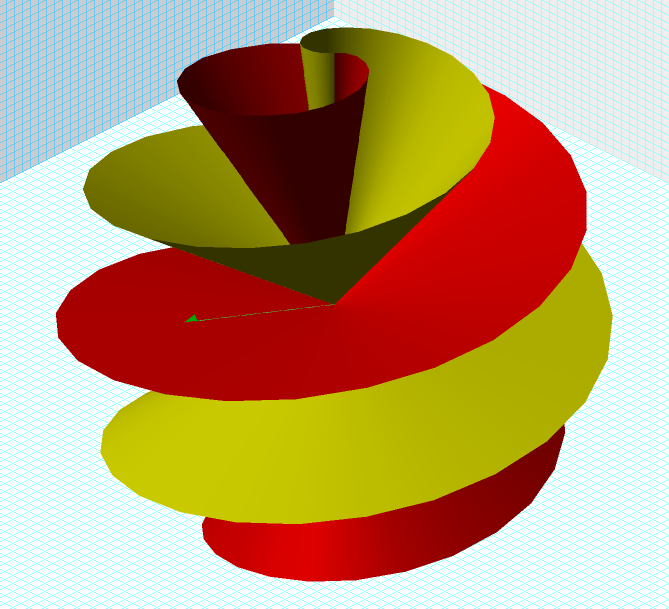
Figure 2. Spiral S∞
The essential difference between these two forms is that one spirals about the polar axis and the other spirals about the equator. They differ in the transposition of v and u in the phi term. (The use of pi in the phi term of the conch is optional.)
Figure 3 Spiral and Conch
Click picture for movie.
Click "BACK" to return
THE CONCH AS SPIRAL
Another difference is that unlike the S∞ , the conch does not have flat straight line radii. We rule that the conch, like the S∞, be unique, not self contradicting. This means it may not penetrate itself. However, its negative is a separate form and may penetrate the positive. This was also allowed for S∞. The conch is a continuous curved surface. It does not cross itself and is not self contradicting. It spirals out from a center. There is no outwards limit, just had to stop somewhere for illustration purposes. In this case, it is the upper value of u. The amount of the twist is dependent upon the variable, n.
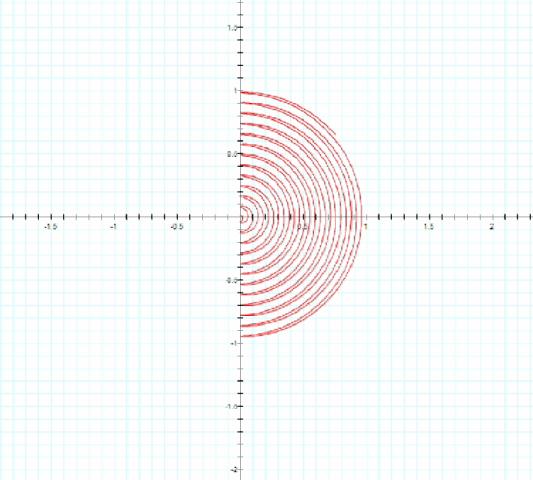
Let's look at the linear version. The parameter is t. x=t*sin(n/t) and y=t*cos(n/t)
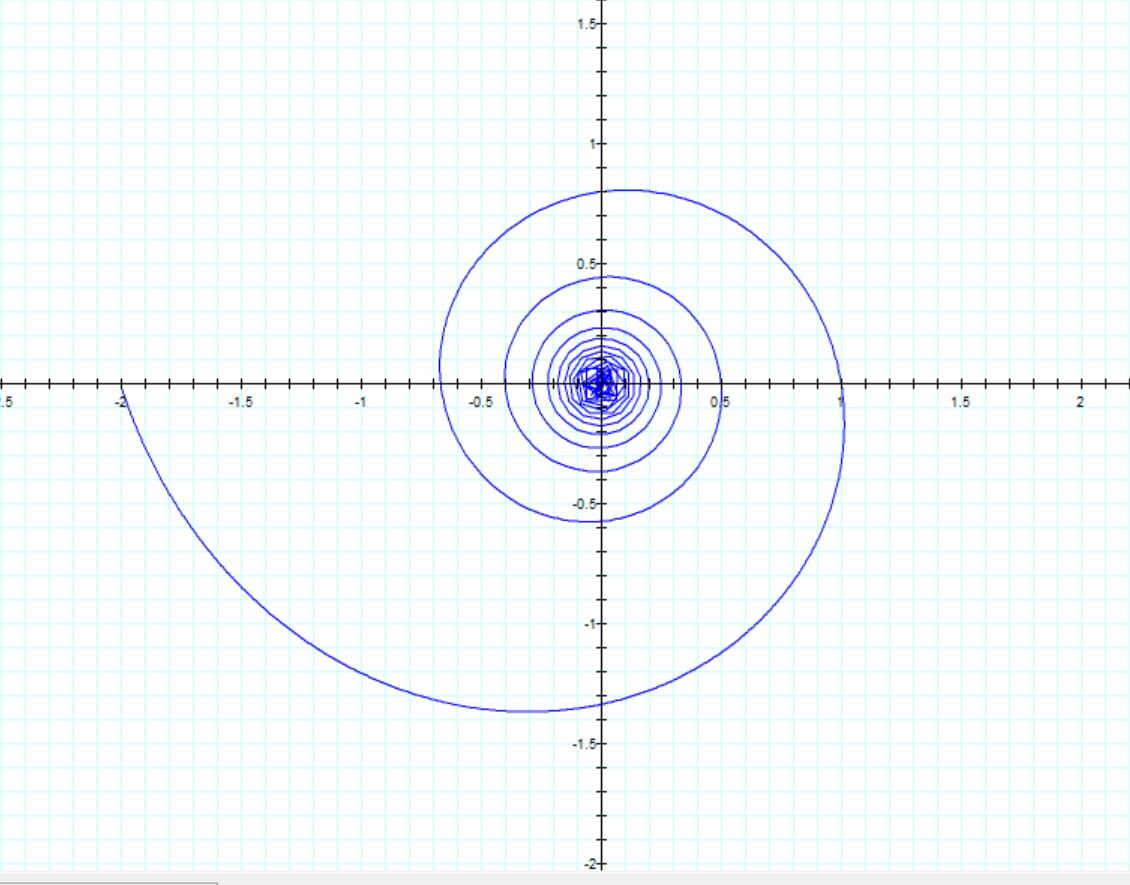
Figure 4. Conch In Two Dimensions Is A Flat Spiral.
Note on graphics: The graphics engines I have available cannot resolve the spiral near the center. They interpolate straight line chords instead of curves.
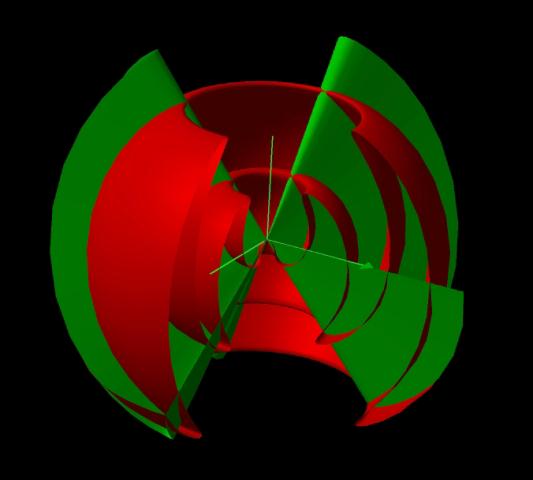
To develop the conch, the spiral is rotated about an axis. To illustrate what is happening in the 3d figure, let us first look at a 1/6th slice. A thinner band from a sphere (yellow) has been provided as a reference.
The spiral extends to the upper limit of u, the maximum radius. That is true no matter how tightly wound it is or how great the radius. There is no upper limit in theory as u can be as large as we want.
Figure 5 1/6 Conch Section
Click picture for movie.
Click "BACK" to return
To better illustrate the full rotation, consider these illustrations. These are CAD models (Solidworks). They are similar to wireframes so that you can see what is going on inside. The conch continues spiraling to the center, but the graphics engine cannot handle it. The empty space shown in the center is because the engine will not compute values below t = 0.01. At the origin, the value is NAN, not a number. That is because the parameters can have zero value.
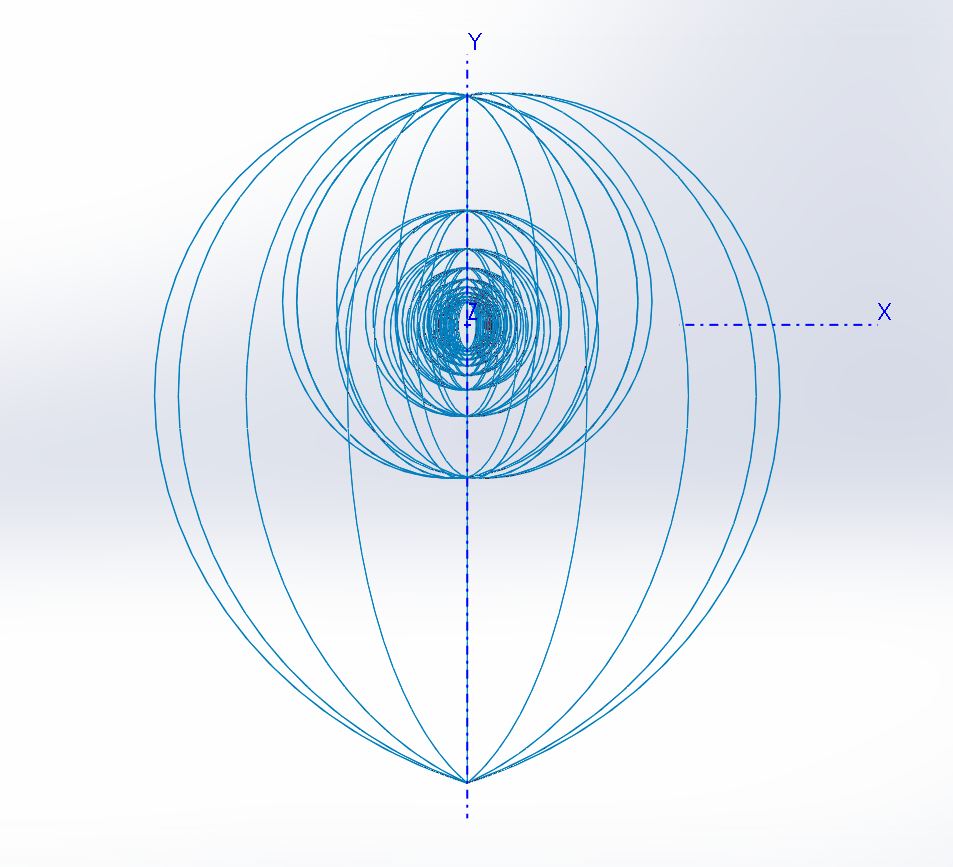
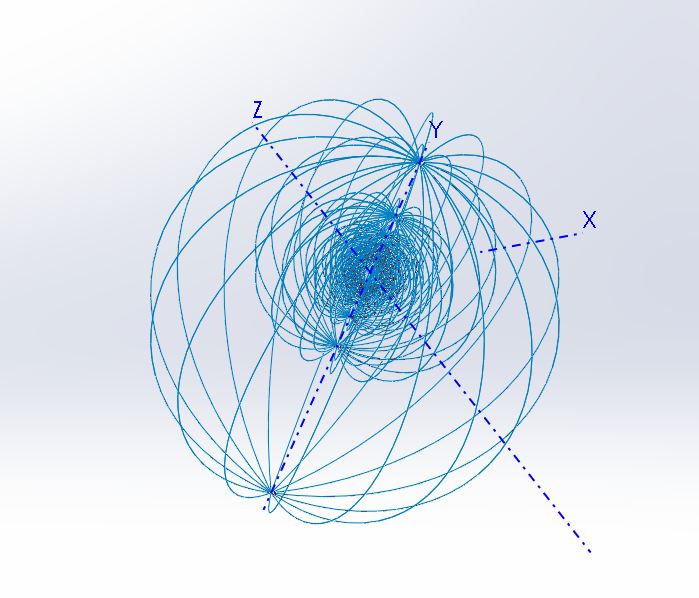
Figure 6a & 6b. Wireframes of the Conch
THE RAIL
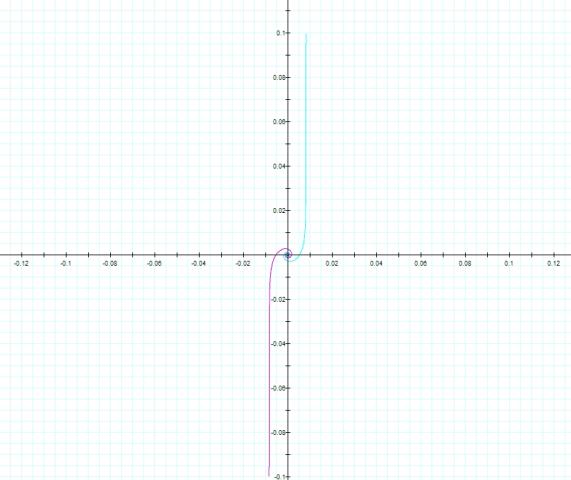
The equation for the rail is no different. It is the beginning stage of the conch. It develops before the conch emerges from u = 0. As y emerges from 0, the curve appears surrounding the vertical axis.
Here is the formation of this from n=0 to n=0.009.
Figure 7 The Rail Emerges At Small Values
Click picture for movie.
Click "BACK" to return
Here is a ½ view as the conch grows from zero. Notice in the animation that a tube is formed at the initiation. It quickly swells out to the curved form. The tube directs the rail.
Figure 8 The Half Conch
Click picture for movie.
Click "BACK" to return
THE NATURE OF THE CONCH- The Imaginary Universe
The S∞ has been defined as space filling. It developed from two dimensional sheets we call "veils". When veils are wound to infinity, they exhibit a density gradient. This yields an infinitely dense point center we term the "nexus". From the nexus radii extend in all directions. Since the nexus is infinitely dense, it cannot exist in the 2d world and transitions into what we would call matter.
The conch however, is not space filling. Of what is it comprised? In the article on Force, we surmised that energy could be stored in imaginary area, i2 . That imaginary area could as well be considered as a patch perpendicular to a radius. So while the conch can be considered the extent of its spiral, it can also be considered the sum of its patches of imaginary area perpendicular to radii from a center. The radius from the center to any patch is determined by the formula. The patches curve within S∞, through imaginary volume.
What am I talking about? Like the discussion of force, there is no clear understanding of what energy is. There are volumes written on how to make it and what to do with it. It behaves as though it were traveling through a medium, but one has not been found. I previously wrote that we are observing a 2d phenomenon from a 3d platform. Our view of reality may not be comprehensive as we do not see all that is there. Dark energy and dark matter are the standard terms in modern science but are undefined.
The term "complex number" refers to numbers that have both real and imaginary components. They exist in a world we can define by our number system and one which stems from a system which doesn't quite fit. The imaginary number i, is defined as the square root of -1. Its square is simply -1 and its cube is the negative of the square root of minus -1. Let me propose that these define the space in which energy exists. It is a negative space to our positive world. We have said that the conch is composed of imaginary area, i2 = -1. Its cube, i3 = -i, is what allows the sheet to appear curved in a three dimensional manner.
Unlike the S∞ which is static, the conch is a dynamic form. This offers a model for storing energy, it can grow and diminish as it adds or subtracts i2. It also solves the problem of increasing the energy of a S∞.
In "Force", the exchange of energy is attributed to twistedness. This now gives a firmer definition of that twistedness. It is the conch of particle * transferring twist to particle # in curvilinear currency. (* and # are used to designate donor and receptor particles respectively.) So, the models I have been working with in the S writings are only a part of a very dynamic picture. They are a state of being which locates the saddle relative to the rest of the universe. The conch is the twistedness. It is the energy storage device. The rail is the energy transmitting device. In the description of S∞ , we said that the nexus moves, not the veil. The nexus is the term for the point center of the S. The conch moves with the nexus.
HOW THE RAIL TRANSMITS ENERGY
Here is a way for the rail to transmit this twistedness. The conch exists in complex negative space as a two dimensional curved sheet. It has both real and imaginary components. It diminishes towards a line as the variable n approaches zero. The real part disappears as the variable n becomes zero. This leaves the imaginary part as a line. It is a one dimensional phenomenon carrying the twistedness, as if the little conch has condensed. When it reaches a receptive #, the process reverses. The conch ball reforms at the other end.
We allow the conch to calve off the energy to be transferred. Those are the smaller conches in figure 9. Consider the calf on the left, with the larger conch, to be diminishing. The one on the right is taking in the rail and expanding. Remember that the conch has no particular size limit. The calf can then occur within it and send a rail from there. Conches can overlap. Space is filled with them and their calves and the rails exchanging energy.
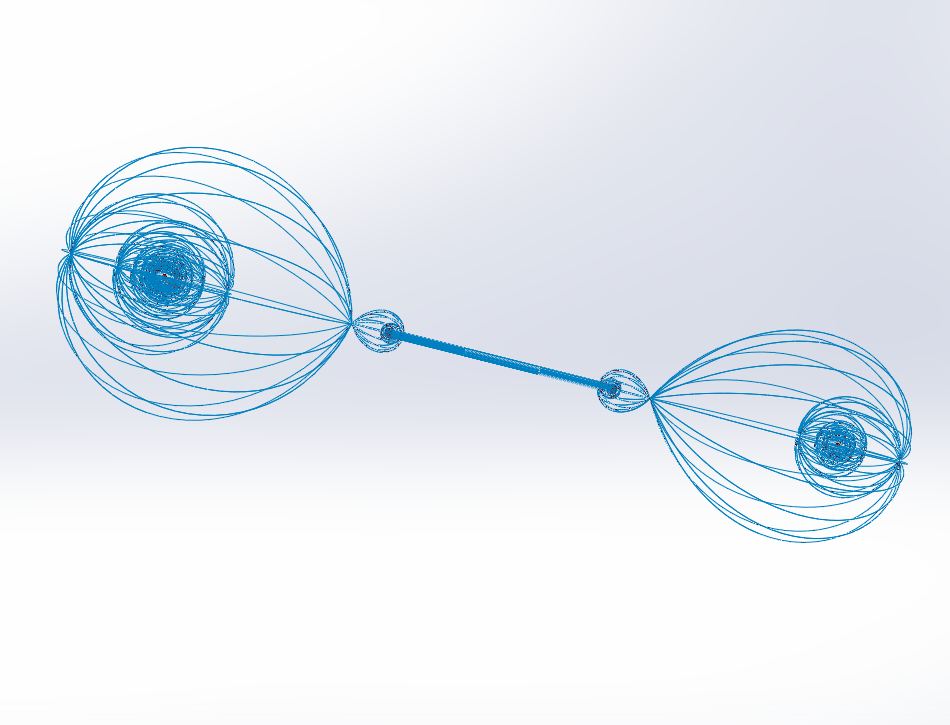
Figure 9. The Rail.
Recall the conches of both # and * reside each within their own Saddlemniscus. Those are not shown in Fig. 9 for clarity.
THE RUFF-ONION DUO
The conch provides only part of this exercise. The ruff was also introduced as a form of S∞. It has a corresponding form also, the onion.
ONION

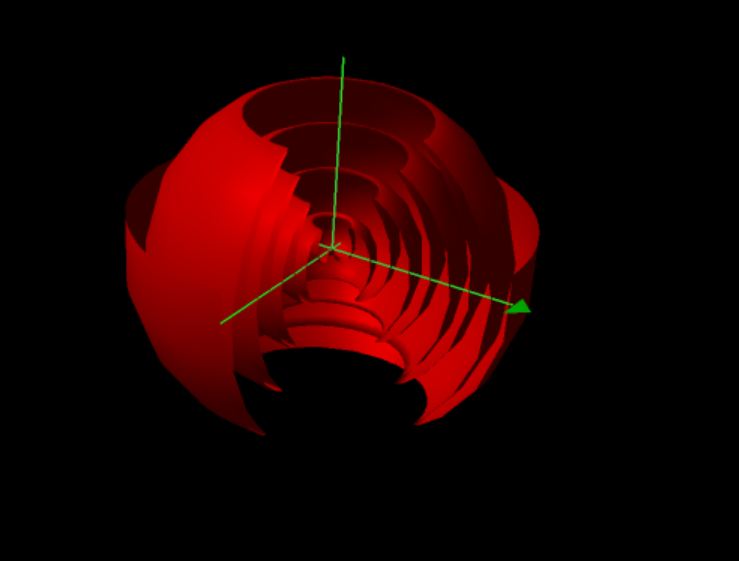
Figure 10 The Onion
RUFF
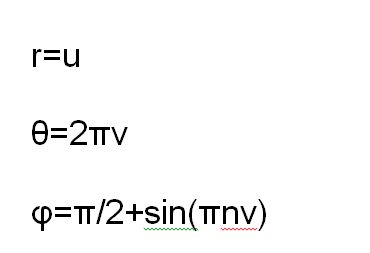

Figure 11. The Ruff
Once again, they differ only in the transposition of v and u in the phi term. They also differ in that one spirals about the polar axis and the other spirals about the equator.
Figure 12 The Ruff and Onion
Click picture for movie.
Click "BACK" to return
Figure 13 The Onion Changes Frequency
Click picture for movie.
Click "BACK" to return
Again, let's look at the linear version. The parameter is t. The factor pi/2 is only used to drive the form to the vertical axis. The waves do close at the top as this 2d animation shows. Frequency is animated here.
x=t*cos(pi/2(cos(nt))) and y=t*sin(pi/2(cos(n/t)))
Alternatively in polar coordinates, r=t and theta= pi/2cos(nt).
The onion also differs from the conch at its base state, x = 0. Y does not vanish as it does with the conch. It becomes a straight line at the vertical axis. At their inception, the conch and the onion form the pair of 0 and 1, the base duality. Like positive and negative, the one fulfills the other. How does this affect the concept of energy transmission? That we will explore later.
Here is a wire frame view. It appears to have several poles along the axis. The pi/2 factor drives it to a 180 degree sweep in figure 13. That is simply one harmonic as it can have many, such as in figure 12.
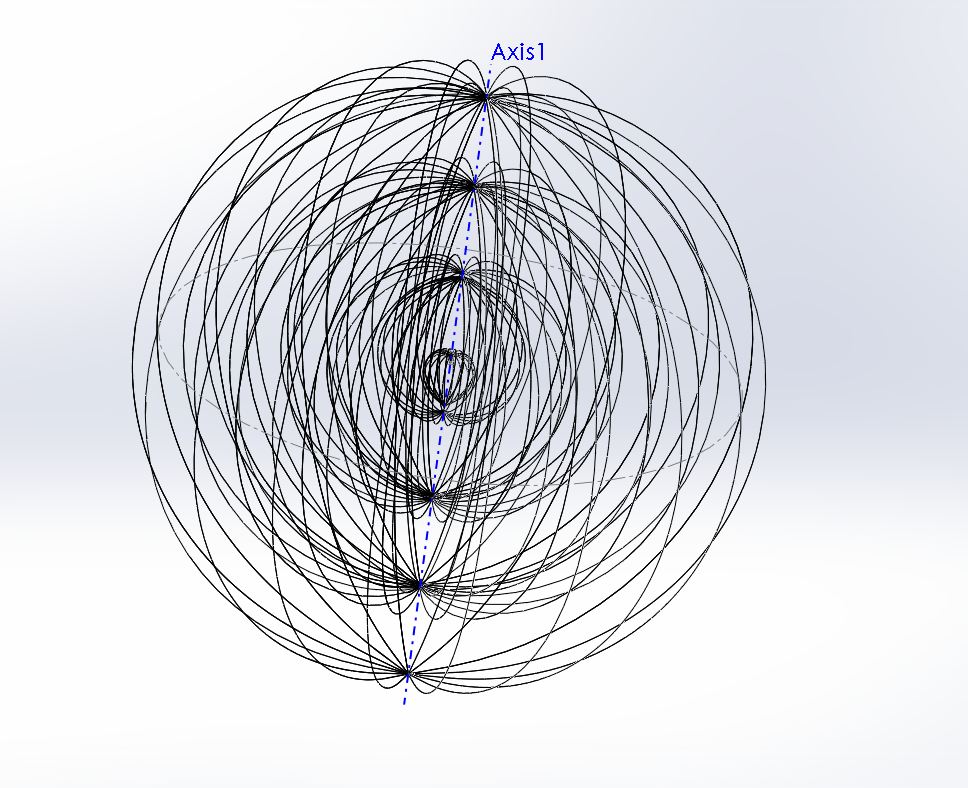
Figure 14. Onion Wireframe.
RETURN TO:
M2 Solids Homepage
Science and Math Homepage